(5)誤差の伝播
■誤差の計算
計算機での算術演算の基本は加減乗除です。
加減乗除での誤差は以下のようになります。

■領域算術
X1=10±1,X2=10±1として,X1とX2の演算結果の最大・最小は
以下の表のとおりとなります。
| 演算 |
区分 |
誤差の計算 |
最大
最小差 |
| 加算 |
最大 |
11 + 11 = 22 = 20 + 2 |
4
|
| 最小 |
9 + 9 = 18 = 20 - 2 |
| 減算 |
最大 |
11 - 9 = 2 = 0 + 2 |
4 |
| 最小 |
9 - 11 = -2 = 0 - 2 |
| 乗算 |
最大 |
11 * 11 = 121 = 100 + 21 |
40 |
| 最小 |
9 * 9 = 81 = 100 - 19 |
| 除算 |
最大 |
1 / 9 = 1.2222 = 1 + 0.2222 |
0.4040 |
| 最小 |
9 / 11 = 0.8181 = 1 - 0.1818 |
しかし,すべてが危険側になるとは限りません。
誤差を打ち消すケースもあります。
■誤差分布
連続的な加算を考えて見ましょう。
最初の数の最後の桁の数が+1または−1の四捨五入の誤差を
持っているものとします。
この2つの状態を次のように書くものとします。
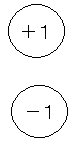
次の数も同様に,最後の桁の数が+1または−1の四捨五入の誤差を
持っているものとしますと,加算によって次のような状態になりえます。
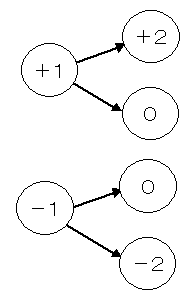
すなわち, 0の状態が2個,+2が1個,−2が1個
となっていますので,
このことを次のように表現することとしましょう。
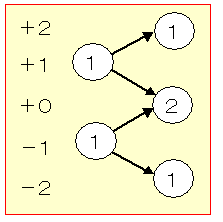
2番目の加算では,次のようになります。
いわゆる,パスカルの三角形の形で進行します。
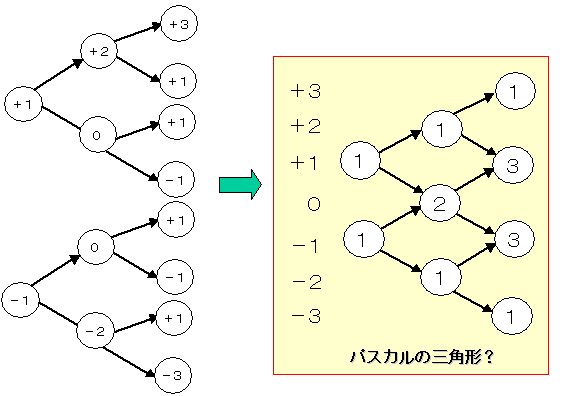
3番目,4番目と進むと,以下のように中央部分の頻度が
多い傾向になっていきます。
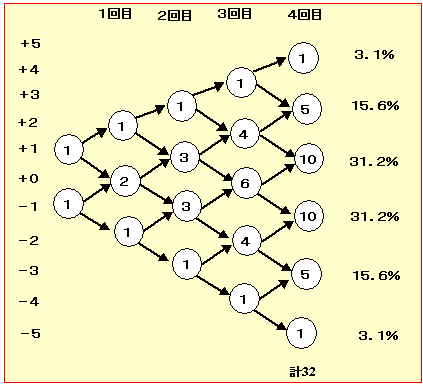
すなわち,最大,最小の誤差の頻度は少なくなっていきます。
|