（６）モデル化による誤差

■誤差の評価

　ここでは，差分近似における数値拡散の例を取り上げます。

たとえば，流れによる輸送方程式において，


差分近似すると，

　
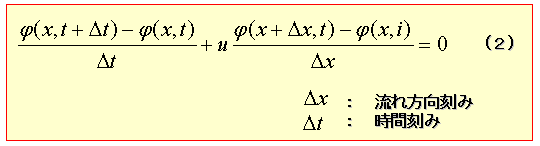
（注）以下，式の展開が苦手な人は，関数の２次の項まで
　　　テーラー展開した式を最初の式に代入すると，
　　　元の式になかった項が現れるということを理解しましょう。
　　　以下は，その理由付けです。


　


　　
　　　　　

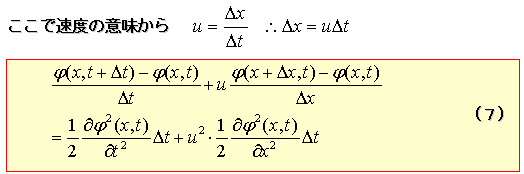
■誤差の解釈

　元の式と比べてみると，差分で近似した結果，

本来の数式や現象になかった項があたかも存在するかのように

現れています。すなわち，有限の時間間隔，有限の区間の差分で

近似すると，２階微分の項が付加されることになります。

　この項を拡散項といいます。この項は，

　　運動量の場合→粘性係数
　　熱量の場合　→熱伝導係数
　　物質の場合　→拡散係数

等に相当する量です。

　なお，拡散項は， 数値解析の都合上出てくる量であり，

物理的に存在する量ではないことに注意して下さい。