(3)数値解析における計算上の注意
■整数の桁あふれ
計算機における整数は,有限の桁からなりますから,
表現できる値には限界があります。
この限界を超えることを桁あふれといいます。
・2バイト整数 -32,768 〜 +32,767

・4バイト(32ビット)整数 -2,147,483,648
〜 -2,147,483,647

■小数(浮動小数点)2進数表現
浮動小数点数の形式はコンピュータによって異なります。
以下はその1例です。なお,以下の例は4バイト(32ビット)長ですが,
8バイト(64ビット:倍精度)長もあります。
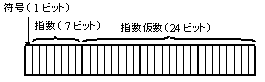
| 符号 |
: 0のとき非負,1のとき負 |
| 指数(n) |
: 2の補数表現(先頭ビットは符号) |
| 仮数(α) |
: 絶対値 1≦α<1 |
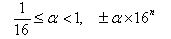
たとえば,
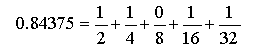
ですから,2進数表記すると
0 000 0000 1101 1000 0000 0000
0000
0000
16進数で表記すれば,00 D8 00 00 となります。
■桁落ち(loss of significant digits)
理解しやすくするため,10進数で例を示します。
a = 0.123456,b = 0.123455 → c
= a - b = 0.00001
a, bは有効数字6桁ですが, cの有効数字が1桁になってしまいます。
■丸め誤差(round-off error)
理解しやすくするため,10進数で例を示します。
a = 12.3456789,b = 12.3456666
c = a - b = 0.0000123
x = 0.123 / c = 10000
ここで,小数点以下4桁までとして四捨五入すると
a = 12.3457,b = 12.3457
c = a - b = 0
x = 0.123 / C = ∞ (ゼロ割)
■打切り誤差
テーラー展開等で関数値を求める際,無限に計算することができないので,
途中で計算を打ち切らざるをえません。これによる誤差を打切り誤差といいます。
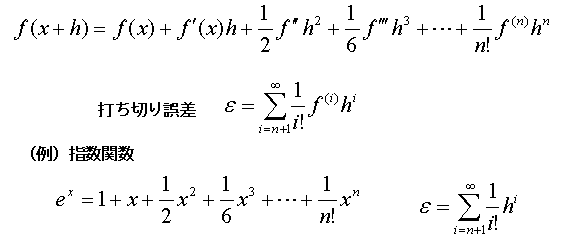
|