（１）なぜ誤差が問題となるのか？

　数値解析では，次のような理由から誤差の問題が大きな鍵となります。
　(a) 数値解では，解を求めるために仮定や近似を行うので，
　　　厳密な解の値を求めることはほぼできない。

　(b) コンピュータの実数は有限の桁で表現した近似値である。

　(c) 演算する前に近似された値（例えばπ）を用いている。

　(d) 物理的な数式モデルでも近似が行われている。

　したがって，有用な解を得るためには，
以下の点について明白にしておく必要があります。

　(a) いつ近似がなされたか？

　(b) 近似が解に及ぼす影響はどの程度か

■誤差の発生

　数値解析で誤差が発生するのは，以下のような箇所です。

　(a) 数学モデルを作るために単純化せざるをえないとき

　　　　［例］　実際の気体の摩擦抵抗をシミュレーションする際，
　　　　　　　　式中の相関関係で理想気体の法則を使う。

　(b) 測定装置の限界によるデータの誤差

　(c) 数学モデルの解を求める際の近似

　ここでは，上記(b),(c)を取り扱います。

■解析解でも近似することが多い

　解析的に問題を解く際に，近似することがよくあります。
たとえば，ここでは次のような振り子の問題を取り上げてみましょう。
　　　　　　　　
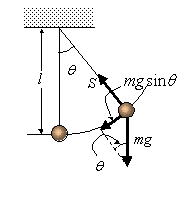
　この問題を解く際，通常，θが小さいものと仮定して，
　　　　
とするのが，通常です。
　この仮定を入れないで，そのまま差分近似すると，
　　　
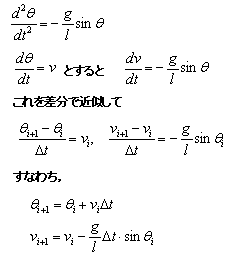
グラフ化すると
　　　　　
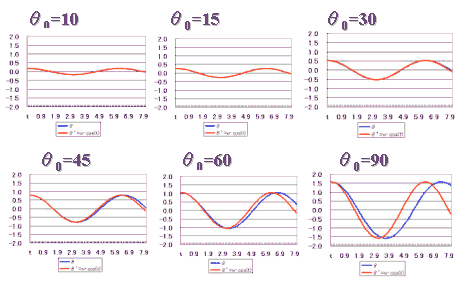
このように，初期値θが大きいと，この仮定は成り立たないことが分かります。
［差分近似してグラフ化したExcel Fileはこちらから］