（４）検討例

　数値解析にあたって検討した例を示します。
この例は，降雨による地表流，地下水流のシミュレーションにおける
有限差分方程式の検討例です。

　流体の微分方程式，

　　

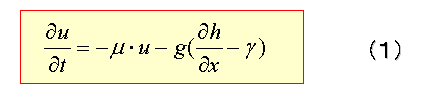
の通常の差分近似式は，

　　　　

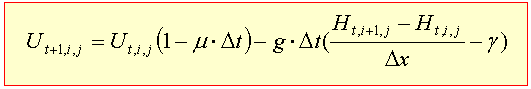
です。一方，Δt　は，前提として微小時間ですが，

我々に与えられる雨量データは時間雨量です。


しかし，Δt　として，時間単位/分単位を与えると，

加速度項が大きすぎて，

１時間刻みで１メッシュを超える速度になってしまいます。

これでは，差分方程式自体が成立しなくなります。


　人工項としての動粘性抵抗を導入したり，

風上差分を適用しても，極めて大きな値になってしまいます。


　一方，地下水流と地表水流においては，

水深あるいは地下水位の勾配の時間変化は

地形の勾配に比べてわずかであるという特徴があります。このことは，


　■水深の時間変化に比べ，地形上の勾配の方が非常に大きい。

　■∂h／∂x　の時間変化はわずかであり，無視できる。


とまとめることができます。すなわち，

とすることができます。

■新たな近似式の導入



■地下水流についての補足

　地下水流については，以下のように考えることができます。

(a) 地下水における基礎方程式は，

　　Darcyの法則を適用すれば，より単純な式となります。

(b) 地表流と同様の近似式を導くことが可能である。


■シミュレーションの実行条件

　画面表示をはっきりさせるために，極端な例を示します。

すなわち，時間雨量５０ｍｍを６００分＋１８０（１３時間降らせてみたら）という

条件で実行してみます。

　　　　　

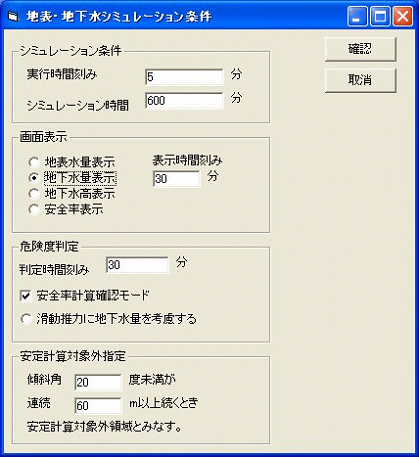
実行画面の例を以下に示します。
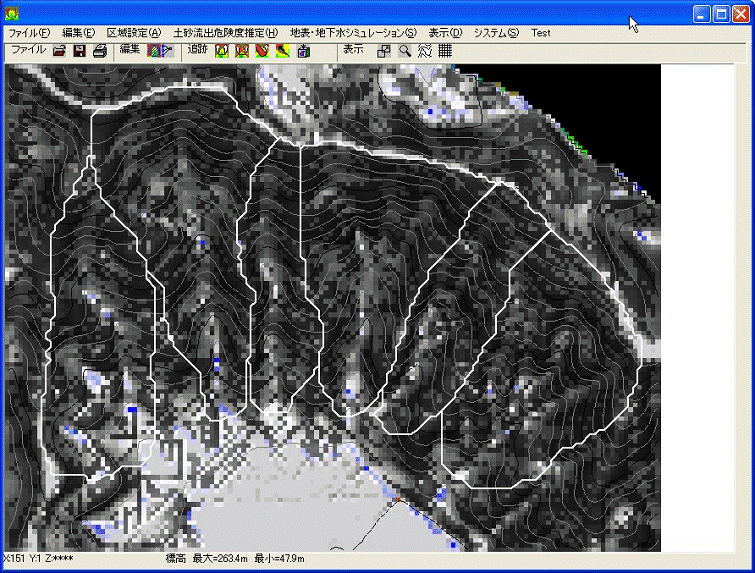